حد، به زبان ساده

خیلی از افراد از ریاضی فراری اند بخاطر دروس سخت اش. که یکی از آنها حد است. هدف من ساده گفتن حد، و امثال آن به عموم است.

یکی از پایه های ریاضیات پیشرفته، و البته یکی از گرایش های ریاضی محض، حد و آنالیز است. حد، همچنین نردبانی بود که بدون آن، حسابان هم هرگز شکل نمی گرفت. پس اگر می خواهید وارد رشته ریاضی فیزیک شوید، برای کنکور ریاضی آماده شوید، مستقل ریاضی را مطالعه کنید، و... قطعا باید حد را کاملا مسلط و بلد باشید.

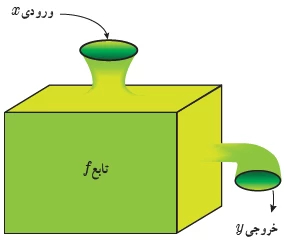
تابع: قبل از هر چیز باید تابع رو بشناسید. داستان تابع این است: یک ماشین کارخانه ای(تابع)، که با دادن یک x(ورودی) به آن، دستگاه تغییراتی روی آن ایجاد می کند و شما y(خروجی) را تحویل می گیرید. برای مثال یک گروه از توابع معروف، توابع مثلثاتی هستند. مانندِ کسینوس که در مثلثات، تابعی است که در یک مثلث قائم الزاویه، اگر یک زاویه دیگر در بین آن دو زاویه دیگر، مثل تِتا(در مثلثات معمولا از تِتا بجای x بعنوان مجهول استفاده می شود) داشته باشیم، آنگاه کسینوس آن زاویه، برابرِ نسبت ضلعِ مجاور(کنار آن زاویه ولی وتر یا بزرگترین ضلع، نه!) بر ضلعِ وتر(بزرگترین ضلع) است! و مثلثات به ما میگه با زوایای ثابتِ تتا، این نسبت یکی از نسبت هایی است که همیشه ثابت است! و با نماد Cos(teta) شناخته می شود. مثلاً Cos(0)=1, و Cos(90)=0. که بعداً در پستی راجب مثلثات و چرایی این اعداد صحبت می کنیم. یا تابع فرضی و خطی o(x)=2x-1, x امین عدد فرد به شرطِ x طبیعی را می گوید.

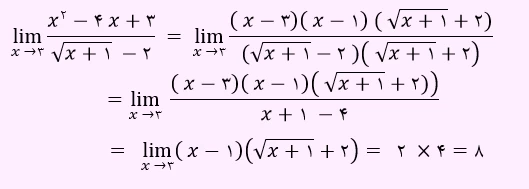
تعریف حد: حالا که تابع رو بلد هستیم، وقت آن است که حد را یاد بگیریم مگه نه؟ بله. ولی شاید برایتان سوال پیش بی آید حد، اصلاً از کجا بوجود آمد؟ خب، باید بگم‌ ریاضی دانان فهمیدند یک سری از محاسبات هستند، که نمیتونیم دقیق محاسبه کنیم شان. بین خود نشستند و به دنبال راهی برای این مشکل بودند، که، حد به ذهن شان رسید! گفتند: اگر نمی شود گفت این محاسبات برای فلان تابع و فلان عدد جواب اش چیست، شاید بتوانیم بگوئیم با مایل شد فلان عدد در این تابع، جواب به آن میل می کند! و اینجا بود که بی نهایت، جا پای بزرگی برای خودش در ریاضیات وا کرد. به زبان ساده، حد، یعنی در تابع f(x), اگر x به a میل کند، f(x) به چه میل می کند؟ که به زبان ریاضیاتی اینجوری نوشته می شود:(عبارتِ (x➡️a) البته معمولاً پائین کلمه lim یا مخفف Limit قرار می گیرد و فلش یعنی از x به a می رویم) lim(x➡️a) f(x) مثلاً، این حد را حل کنیم: lim(x➡️10) x^2=? خب، این یک مثال بسیار ساده است و در واقع اصلا نیاز به حد ندارد. وقتی x به 10 مایل می شود، x^2 هم به 10^2 یا 100 مایل می شود. پس جواب این حد 100 است. حالا بیاین یک حدِ چالشی تر و معروف تر را حل کنیم. lim(x➡️0) 1/x=? خب، شما نمی توانید مثل سوال قبلی مستقیماً 1 را تقسیم بر ۰ کنید چون تقسیم بر ۰ تنها در حد معنا دارد! خب، بچه ها، ما می دانیم هر چه x, کوچکتر می شود، این جواب بزرگتر می شود، مگر اینکه به اعداد منفی برسیم که جواب را منفی می کند. 0, دقیقا مرز بین مثبت و منفی است، پس کوچکترین عددِ نا منفی است! و ما گفتیم هر چه مخرج کوچکتر، بزرگتر، مگر اینکه منفی شود! پس کوچکتر از این در بین اعداد نامنفی نمی توان یافت. و این یعنی بزرگترین عددِ ممکن! که هیچ عددی از آن بزرگ تر نیست. و این، دقیقا تعریف بی نهایت است! پس این حد به بی نهایت مایل می شود.

چند حدِ معروف در ریاضیات: lim(x➡️♾) (1+a/x)^x=e^a (e یا ثابت نپر، یک ثابتِ مهم در ریاضیات و گنگ مثل عدد پی است. و حدود 2.718... است) lim(x➡️♾) (1/x)=0 (دقیقا برعکس حالتی که در اسلاید قبل حل کردیم. هر چه مخرج بزرگتر می شود، جواب کوچکتر می شود. ولی می دانیم هرگز منفی نمی شود جواب در تقسیم زیرا هم صورت و هم مخرج، مثبت اند. و کوچکترین عددِ نامنفی چیست؟ 0) lim(x➡️90) tan(x) =♾ (این هم در پست های بعدی در مورد مثلثات، توضیح می دهم چرا. زیرا تانژانت تابع مثلثات است) و ...

امیدوارم از اولین پست ام خوشتان آمده باشد. اگر نقدی یا پیشنهادی دارید یا می خواهید پست های بعدی ام راجب موضوع دانشگاهی دیگری باشد، لطفا بنویسید تا اگر نمی دانم، یا اشتباه توضیح دادم، از شما بزرگواران یاد بگیرم. ممنون.