فرضیه ریمان چیست؟

مهم‌ترین مسئله‌ی حل نشده در ریاضیات محض به فرضیه ریمان (Riemann Hypothesis) مشهور است. این مسئله را برنهارت ریمان، ریاضیدان آلمانی قرن نوزدهم مطرح کرده است که آثارش در زمینه آنالیز و هندسه دیفرانسیل، پایه ریاضی نظریه‌ی نسبیت عام شد.

فرضیه ریمان از سال ۱۸۵۹ تاکنون حل نشده باقی مانده و به‌قدری دشوار است که دیوید هیلبرت، از تأثیرگذارترین ریاضیدانان در پیدایش و گسترش مکانیک کوانتومی و نظریه نسبیت، درباره‌ی آن گفت:‌ اگر قرار بود بعد از هزار سال از خواب بیدار شوم، اولین سوالی که می‌پرسیدم این بود: آیا فرضیه ریمان اثبات شده است؟

جالب است بدانید هیلبرت در سال ۱۹۰۰، بیست و سه سؤال ریاضی که تا آن زمان حل نشده بودند را مطرح کرده بود که فرضیه ریمان یکی از آن‌ها بود. برخی از این سؤال‌ها که به مسائل هیلبرت شهرت دارند، حل شده‌اند و تأثیر بسزایی بر ریاضیات قرن بیستم گذاشتند.

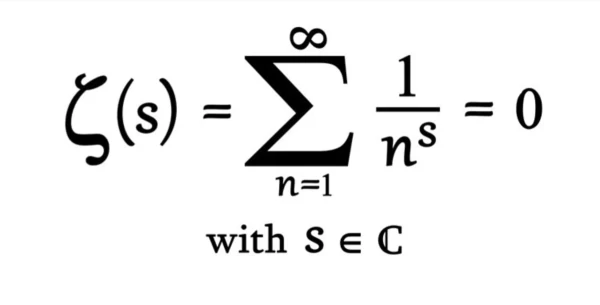
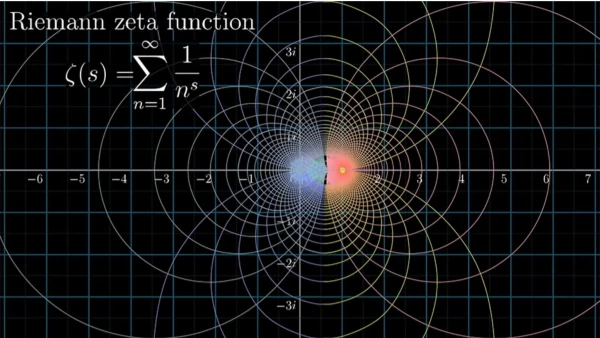
فرضیه ریمان درواقع از شما می‌خواهد اثبات کنید تابع زتا ریمان در چه شرایطی برابر با صفر است. این تابع در ظاهر، ساده به نظر می‌رسد؛ اما پیچیدگی آن روی نمودار ظاهر می‌شود. برای مثال، به نمودار |ζ(1/2+iy)| (محور عمودی) به‌عنوان تابعی از y (محور افقی) نگاه کنید. همان‌طورکه می‌بینید، تابع زتا برای مقادیر ۱۴، ۲۱، ۲۵ و الی‌آخر روی محور افقی، به صفر نزدیک می‌شود. به این‌ها صفرهای تابع زتا می‌گویند و از اهمیت بسیاری برخوردارند، چراکه رفتارشان هیجان‌انگیز است. فرضیه ریمان هم درواقع گزاره‌ای درباره‌ی نحوه توزیع این صفرها است. ریمان می‌گوید تابع زتا تنها زمانی به صفر می‌رسد که با اعداد صحیح زوج منفی و اعداد مختلط با قسمت واقعی ۱/۲ سروکار داشته باشیم. مشکل اینجا است که اگرچه بیش از ۲۵۰ میلیون صفر این فرضیه را اثبات کرده‌اند، هنوز ثابت نشده که این موضوع برای تمام صفرها صدق می‌کند.

فرضیه ریمان از این جهت بسیار مهم است که اعداد اول (که فقط بر یک و خودشان تقسیم‌پذیرند) اساسی‌ترین و اسرارآمیزترین مفهوم در ریاضیات هستند. وقتی اعداد اول را به صورت مجموعه خطی پشت سر هم می‌نویسیم، هیچ الگویی در نحوه توزیع آن‌ها ظاهر نمی‌شود و به‌همین خاطر نمی‌توانیم تمام اعداد اول را پیش‌بینی کنیم. اما وقتی این اعداد را به کمک تابع زتا ریمان روی نمودار می‌آوریم، الگوی جالبی از صفرهای ریمان روی آن ظاهر می‌شود که اگر بتوانیم آن را برای تمام اعداد ثابت می‌کنیم، آن‌وقت می‌توانیم بگوییم الگوی پنهان توزیع اعداد اول را سرانجام کشف کرده‌ایم. بدین‌ترتیب می‌توانیم با دقت بسیار بالا تعداد اعداد اول در هر بازه معینی را تعیین کنیم.

شاید بپرسید داشتن تابعی برای تعریف اعداد اول اصلاً چه اهمیتی دارد؟ بسیاری از ریاضیدانان اعداد اول را به‌عنوان اتم‌های تشکیل‌دهنده‌ی تمام اعداد دیگر می‌بینند، زیرا می‌توانید با استفاده از اعداد اول به هر عددی برسید. در فرضیه ریمان، دامنه‌ای که روی خط عددی از مقادیری ایجاد می‌شود که تابع زتا را صفر می‌کند، همانند فواصل بین سطوح انرژی در سیستم‌های کوانتومی است و این یعنی نوعی رابطه بین اجزای سازنده اعداد با اعداد اول و اجزای سازنده ماده با اتم وجود دارد و حل این فرضیه ما را به درک جدیدی از ماده خواهد رساند.