اگر بتونی این مسئله رو اثبات کنین میبرین اگر دو خط موازی را یک خط مورب قطع کند آنگاه ۸ زاویه پدید می آید که همه ی زوایای حاده با همای زوایای منفرجه با هم برابر اند
| اتمام مسابقه | 1404/09/26 |
| ظرفیت مسابقه | 10 شرکت کننده |
| نحوه تعیین برنده | بدون مدال مسابقهتوسط سازنده مسابقه |
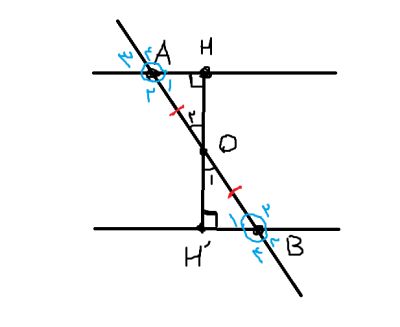
ما می آییم HH' رو عمود بر دو خط موازی رسم می کنیم به طوری که خط AB رو دقیقا نصف کنه پس AO=OB این از این. از اونور O1=O2 بخاطر اینکه متقابل به راس اند. حالا دو مثلث AHO و BH'O با هم همنهشت اند با خاصیت وتر و یک زاویه تند. پس اجزای متناظر باهم برابرند پس A1=B1. از اونر بخاطر متقابل بع راس بودن A3=A1 و B1=B3. پس A1=B3=A3=B1 . از اونور همه اونای دیگه مکمل اینان و مکمل زاویه های برابر، برابرند. پس A2=A4=B2=B4 . داداش برا ما سمپادی ها اینا چیزی نیست که
داداش، من کلاس جهارمم
ریاضی نهم فک کنم اگر دو خط موازی را یک خط مورب قطع کند، زاویههای متناظر برابرند و زاویههای متقابل به رأس نیز برابرند. از آنجا که در هر تقاطع دو زاویه حاده و دو زاویه منفرجه داریم، برابری زاویههای متناظر باعث میشود همهی زوایای حاده برابر باشند و همهی زوایای منفرجه نیز برابر باشند خلاصه منطقی: زاویههای متقابل به رأس برابرند زاویههای متناظر در خطوط موازی برابرند⟹ همه زوایای همنوع (حاده یا منفرجه) برابرند
لینک کوتاه
توجه!
محتوای ارائه شده در این سایت توسط کاربران تولید می شود و تستچی نقشی در تهیه محتوا ندارد بنابراین نمایش این محتوا به منزله تایید یا درستی آن نیست. مسئولیت محتوای درج شده بر عهده کاربر سازنده آن می باشد.

نظرات بازدیدکنندگان (0)